Infografía sobre a historia da clepsidra

Traballo feito polo alumnado de primeiro da ESO empregando as ferramentas do paquete IMS xerado para a alfabetización informacional.

INFOGRAFÍA

Película

Película feita polo alumnado en relación co proxecto

Augateca. A Sacra Orde do ALFIN. En youtube. CC-BY-SA

Deseño 3D e impresión.

Deseño e impresión 3D

Clepsidra

O programa empregado foi Freecad. Para o deseño da clepsidra deselvolvemos o seguinte script en  python, que dende a consola de python de Freecad permitiunos acadar o boceto que revolucionado xera a clepsidra.

Script

x1=0
x2=0.1
y1=0
y2=0
y3=0
y4=0
for g in range(502):
  y1=(x1**4)*15730.98*0.000000001
  y2=(x2**4)*15730.98*0.000000001
  y3=((x1-2)**4)*15730*0.000000001-2
  y4=((x2-2)**4)*15730*0.000000001-2
  App.ActiveDocument.Sketch.addGeometry(Part.Line(App.Vector(x1,y1,0),
  App.Vector(x2,y2,0)))
  App.ActiveDocument.Sketch.addGeometry(Part.Line(App.Vector(x1,y3,0),
  App.Vector(x2,y4,0)))
  x1=x2
  x2=x2+0.1

Co código xeranse os puntos vermellos da seguinte imaxe, que se completan con liñas que pechan o boceto que xera a clepsidra na súa revolución no eixe vertical.

Simón. Boceto. CC-BY-SA

 Revolucionase:

Simón. Revolución. En youtube. Licenza Youtube estándar.

Soportes laterales

Completando os puntos vermellos xerados co script temos o boceto que xera os soportes laterales, deste xeito a clepsidra vese a través do perfil que a xera.

Simón. Soporte lateral. CC-BY-SA

Extrusión do boceto

 

Simón. Soporte lateral. En youtube. Licenza youtube estándar.

 Detalles da impresión

Amósase todo o proceso de impresión

   

Simón. Proceso. En youtube. Licenza youtube estándar

Letras e inscrutacións

As letras son extrusións de camiños feitos co programa Inkscape, empregando tamén operacións booleanas de corte. Os buratos onde encaixan fanse fusionando a letra e o soporte lateral, lévase a letra o sitio onde ten que encaixar, aplícaselle a letra un offset de 0,5 milímetros, córtase a base e o offset, e logo córtase a base e a letra. O proceso amósase no seguinte vídeo.

Simón. Letras. En youtube. Licenza youtube estándar.

Soporte superior

Vexámos un vídeo onde se amosa parte do proceso de impresión.

Simón. Techo. En youtube.Licenza youtube estándar.

Logo e patas.

Este e o traballo do alumnado de segundo e terceiro da ESO.

 Simon. Logo y Patas. En youtube. Licenza youtube estándar.

Tempo de vaciado dunha semiesfera.

Tempo de vaciado da semiesfera.

O aprendido no desenvolvemento matemático  da cleosidra serve para facer cálculos como o tempo de vaciado dunha semiesfera. Aprendemos novamente a sumar empregando o cálculo de segundo de bacharelato.

Desenvolvemento da tarefa.

Supongamos que tenemos una semiesfera llena de agua.

Simón. Semiesfera. CC-BY-SA

Nun instante de tempo determinado o nivel de líquido atoparase a unha altura $y$ sobre o eixo de abscisas. Nese instante a velocidade de saída de líquido polo buraco de evacuación é $\sqrt{2gy}$. Se este buraco ten un radio $r$, o volume de líquido evacuado nun tempo moi pequeno $dt$ será: 

$\pi r^{²} \sqrt{2gy}  dt$

Sabemos que se cumpre a seguinte relación, chamando ao radio R = 5cm:

$(R-y)^{²}+x^{²}=R^{²}$ 

de esta ecuación obtemos:

$x=\sqrt{2Ry-y^{²}}$

no transcurso do pequeno tempo $ dt$ o nivel de líquido descenderá unha altura moi pequena, $ dy$. O volume de líquido que se corresponde con ese descenso do nivel é:

$\pi (2Ry-y^{²}) dy$ 

O volume de líquido  da expresión:  $\pi r^{²} \sqrt{2gy}  dt $   é igual ao volume de líquido que se corresponde co da expresión: $\pi (2Ry-y^{²}) dy$  , por tanto:

 $\pi r² \sqrt{2gy} dt=\pi (2Ry-y²) dy$

Para a nosa altura de líquido $y$, nun cambio de tempo $dt$ o nivel de líquido descende $dy$. A variable $y$, $dt$ e $dy$ relaciónanse a través da ecuación diferencial: $\pi r^{²} \sqrt{2gy} dt=\pi (2Ry-y^{²}) dy$. Buscamos calcular o tempo de evacuación de todo o líquido contido na semiesfera. Na  ecuación  $\pi r^{²} \sqrt{2gy} dt=\pi (2Ry-y^{²}) dy$ despexamos $dt$:

$dt=\frac{\pi (2Ry-y^{²})}{\pi r^{²} \sqrt{2gy}}dy$

Esta ecuación dános o tempo dun pequeno descenso de nivel $dy$, partindo dunha altura da auga sobre o eixo de abscisas de valor $y$. Se tuviesemos unha expresión: $dt=\frac{\pi (2Ry-y^{²})}{\pi r^{²} \sqrt{2gy}}dy$  para cada valor de $y$, partindo dun tempo cero ata o tempo de baleirado, e as sumásemos membro a membro todas, teríamos o tempo de baleirado, que sería a suma de todos os $dt$ que se corresponden con cada altura. Ese tempo sería igual á suma de todos os produtos $\frac{\pi (2 Ry-y^{²})}{\pi r^{²} \sqrt{2 gy}} dy$, un para cada altura. A suma de todos eses pequenos tempos, un para cada altura, que representa cada un o descenso no nivel de líquido $dy$ exprésase así:

$\int_{0}^{T}dt$ 

Os números 0 e T representan o valor inicial e final do tempo. O mesmo valor obtemos a través da outra suma:

 $\int_{0}^{R} \frac{\pi (2Ry-y^{²})}{\pi r^{²} \sqrt{2gy}}dy$

O valor inicial de $y$ é 0, e logo de baleirarse a clepsidra o valor de $y$ será R, na suma consideramos que a $y$ increméntase cara abaixo. As operacións que  apréndense a calcular en segundo de bacharelato. Imos resolvelas:

$\int_{0}^{T} dt=T$ 

$\int_{0}^{R} \frac{\pi (2Ry-y^{²})}{\pi r^{²} \sqrt{2gy}}dy=\frac{1}{r^{²} \sqrt{2g}}\left[\int_{0}^{R} 2Ry^{\frac{1}{2}}dy-\int_{0}^{R} y^{\frac{3}{2}}dy\right]=\frac{14 R^{\frac{5}{2}}}{15 r^{²} \sqrt{2g}}$

O tempo de baleirado da semiesfera é:

$T=\frac{14 R^{\frac{5}{2}}}{15 r^{²} \sqrt{2g}}$

Aplicación móvil. App Inventor

Aplicación móvil. App Inventor.

Utilizando o IDE App Inventor, creamos unha aplicación móbil que nos permitirá accionar a bomba de auga, e monitorar as variables que se relacionan co funcionamento da clepsidra dende unha tablet ou dispositivo android. Imos describir os pasos máis importantes do desenvolvemento. O deseño da interface gráfica da aplicación apréciase na seguinte imaxe. Se non a ves ben fai click na imaxe.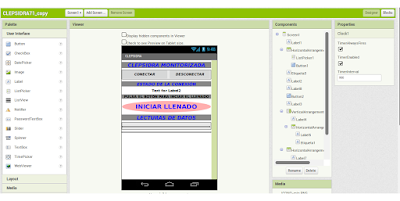

Simón. Deseño. CC-BY-SA

Na seguinte pantalla de App Inventor desenvolvemos a programación do comportamento dos compoñentes que forman parte da nosa interface gráfica. Conseguímolo arrastrando os bloques e uníendolos de forma correcta:

Simón. Programación. CC-BY-SA

imos ver para que serve cada un.

Con esta parte do código inicializamos a screen1.

Simón. Screen1. CC-BY-SA

 Asignamos o listpicker os elementos que nos proporciona o cliente de bluetooth.

Simón. BeforePicking. CC-BY-SA

Conéctase o bluetooth e poñense nas etiquetas a información de conexión o desconexión según o caso.

Simón. AfterPicking. CC-BY-SA

Inicializamos as dúas variables do bucle principal para os datos, e o seu almacenamento nunha lista.

SImón. Variables. CC-BY-SA

Neste bloque temos o bucle principal, no que se asignan ás etiquetas os valores que proceden via bluetooth en relación co descenso do líquido: o tempo transcorrido, a velocidade de descenso do nivel de auga, a distancia ao sensor de ultrasonidos etc...

Simón. Bucle principal. CC-BY-SA

Nestes dous bloques temos os eventos click dos botóns da App, o de desconexión e o de iniciar o enchido da clepsidra que emprega o número 7.

Simón. Eventos click. CC-BY-SA

Circuito electrónico

Circuito electrónico controlado con Arduino

Materiais

Os materiais necesarios son:

• Placa Arduino UNO
• Placa de conexións protoboard
• Un pulsador
• Unha resistencia de 10 k(marrón,negro,laranxa)
• Cable para as conexións
• Un zumbador piezoeléctrico
• Unha resistencia de 100 ohmios
•  Un sensor de distancia por rultrasonidos HC- SRO4
• Un transistor MOSFET IRL540
• Un diodo 1 N4007
• Un motor de CC de 6 a 9V
• Unha resistencia de 1 k(marrón,negro,vermello)
• Unha resistencia de 100 k(marrón,negro,amarelo)
• Módulo bluetooth HC-06

Esquema do circuito 

Fai click na imaxe :

Simón. Circuito. CC-BY-SA

Traballando na montaxe

 

Simón. Circuito. En youtube. Licenza Youtube estándar.

Simulación HTML5

Simulación HTML5

Utilizando o desenvolvemento matemático  imos crear unha simulación informática. Imos poder ver como é a forma das clepsidras e o seu baleirado a través da simulación. Teremos, desta maneira, unha visión moi clara de como é a clepsidra por dentro. Para o desenvolvemento da aplicación imos usar HTML5, o que nos permitirá unha fácil difusión e publicación dos resultados a través de Internet. Os tres linguaxes que integran HTML5 son HTML, CSS e JAVASCRIPT. Usaremos tamén o API Canvas de HTML5 para crear a animación do baleirado.

Imos necesitar unha estrutura de cartafoles como a que se mostra na figura. Fai click co rato para examinala ben.

Eloi. Sitio Web. CC-BY-SA

Isto permítenos separar o código que corresponde a cada linguaxe, HTML, CSS e JAVASCRIPT. HTML define a estrutura da páxina, CSS o estilo e JAVASCRIPT o programa ou script da animación. As frechas negras indican que os elementos que sinalan a outros están contidos neles. Imos desenvolver o código e organizalo nas cartafoles.

Páxina de entrada o sitio index.html

 Para crear esta páxina teclearemos o seguinte código nun editor de texto plano, en Ubuntu o mousepad ou o gedit, en Windows o block de notas. Unha vez tecleado gardarémolo co nome index.html. Este arquivo index.html é a páxina de entrada ao noso sitio. Ao facer dobre click no arquivo, co rato, ábrese o navegador e lanza a nosa páxina web.

<html>
 <head>
  <title>Animación</title>
  <meta http-equiv='Content-Type' content='text/html;
  charset=UTF-8' />
  <link rel='stylesheet' type='text/css'
  href='css/estilos.css'      
   media='screen'/>
 </head>
 <body>
  <div>
  <h1>ANIMACIÓN DE LAS CLEPSIDRAS</h1>
  <p>As clepsidras tendán unha altura de 10cm e
  un buraco para <br/>o
  vaciado de 1mm na súa parte inferior. O facer click no
  <br/> botón preguntarásenos polo tiempo de
  vaciado.<br/>
  Ao teclear un tempo o ordenador xérase a
  clepsidra cuxo<br/>
  perfil responda a ese tempo, según noso
  modelo matemático,
  <br/> e simulará o vaciado.</p>
  <a href='animacion/animacion.html'>
  <img src='imagen/boton.png' /></a>
  </div>
 </body>
</html>

Esta páxina enlaza a través da etiqueta:

 <link rel=' stylesheet' type=' text/ css' href =' css/estilos. css' media=' screen'/>

a folla de estilos estilos. css que se atopa no cartafol css gardada na mesma cartafol que contén a index.html; isto conséguese co atributo: href=' css/estilos. css'; é un exemplo do que se chama direccionamiento relativo. Para crear estilos. css escribimos nun editor de texto plano o seguinte código e gardámolo no cartafol css co nome estilos. css.

 h1 {background-color:#000060;}
div {position:absolute;top:5%;left:20%; border-color:#64009e;
 border-style:solid;border-width:10px;background-color:#00009b;}
h1 {margin:2%;border-color:#64009e; border-style:solid;padding:
5%;border-width:7px;background-color:#8f00e3;}
p {text-align:center;border-color:#64009e; border-style:solid;
margin:5%;padding:5%;border-width:5px;background-color:#8f00e3;}
a {position:relative;bottom:20px;left:40%;padding:20px;}
body {background-color:#000060;}

A animación é enlazada pola páxina index.html a través do atributo href da etiqueta:

<a href='animacion/animacion.html'><img src='imagen/boton.png' /></a>

Ao facer click no botón abrirase a páxina animacion.html que se atopa no cartafol animacion gardada na mesma cartafol que index.html; outro exemplo de direccionamiento relativo. Para escribir a páxina web animacion.html escribimos nun editor de texto plano o seguinte código e gardámolo no cartafol animacion.

<html>
<head>
<title>Animación</title>
<meta http-equiv='Content-Type' content='text/html;
 charset=UTF-8' />
<script type='text/javascript' src='javascript/codigo.js'>
</script>
<link rel='stylesheet' type='text/css'
href='css/estilos.css' screen='media'/>
</head>
<body>
<div id='primera'>
<h2>CLEPSIDRA</h2>
<p>A clepsidra ten 10 centímetros de alto e
un radio no buraco de evacuación dun  milímetro.
 O diseño da clepsidra correspondese co
  tiempo introducido.</p>
<div class='capa1'><H4>TEMPO DE DESCENSO:</H4>
<div  id='reloj2'></div>
</div>
<div class='capa2'>
<canvas id='canvas1' width='550' height='550'>
</canvas>
</div>
</div>
<div id='segunda'>
<h2>CLEPSIDRA</h2>
<p>A clepsidra tien 10 centímetros de alto e
 un radio no buraco de evacuación dun
 milímetro. O deseño da
 clepsidra  correspondese co tempo introducido.</p>
<div class='capa1'><h4>TIEMPO DE DESCENSO:</h4>
<div  id='reloj2'></div>
</div>
<div class='capa2'>
<canvas id='canvas2' width='550' height='550'>
</canvas>
</div>
</div>
</body>
</html>


Esta estrucutura en HTML enlaza cos estilos CSS a través da etiqueta:

 <link rel='stylesheet' type='text/css'  href='css/estilos.css' screen='media'/>

Onde se usa direccionamiento relativo, o procedemento é análogo aos casos anteriores. O código de estilos. css é o seguinte.

body {background-color:#8f00e3;}
#primera {z-index:15; position:absolute; top:1em; left:1em;}
#segunda {z-index:5; position:absolute; top:1em; left:1em;}
.capa1 {float:left;}
.capa2 {position:absolute; top:100px; left:300px;}

A su vez la página animacion.html enlaza el código javascript que realiza la animación, lo hace a través de la etiqueta:

<script type='text/javascript' src='javascript/codigo.js'></script>

Usamos o direccionamiento relativo. O código do arquivo codigo. js móstrase a continuación, e debe estar gardado no cartafol javascript, que está gardada na cartafol animación.

var radio,altura,constante,x1,x2,y1,
y2,rmax,contador,tiempo,bucle;
tiempo=0;
radio=0.001;
contador=0;
altura=0.10;
bucle=true;
while (bucle==true){
  tiempo=prompt("Introduce el tiempo,
  entre 30 segundos y 180 segundos:  ");
  if (tiempo<=180 && tiempo>=30)
    {bucle=false;}
  else
    {bucle=true;}}
constante=(Math.pow((altura/tiempo),2)/
(2*9.81*Math.pow(radio,4)));
rmax=Math.round(Math.pow((altura/constante)
,1/4)*1000*5)+10;
window.addEventListener("load",eventWindowLoaded
,false);
function eventWindowLoaded()  {
  opecanvas();
   }
function opecanvas() {
  var canvasli=document.getElementById('canvas1');
  var contexto=canvasli.getContext('2d');
  var canvasli2=document.getElementById('canvas2');
  var contexto2=canvasli2.getContext('2d');
  setInterval(opedibujar,(tiempo/500)*1000);
  function opedibujar(){
    contexto.clearRect(0,0,500,500);
    contexto.strokeStyle='black';
    contexto.lineWidth=5;
    contexto.fillStyle='red';
    contexto.beginPath();
    x1=0;
    x2=0.2;
    y1=0;
    y2=0;
    for(var i=0;i<=rmax;i++){
      y1=(Math.pow(x1,4)*0.000000001*constante)*5
      y2=(Math.pow(x2,4)*0.000000001*constante)*5
      if (i==0){
        contexto.moveTo(260,500);}
      if (i==rmax){
        contexto.lineTo(i+260,502);
        contexto.lineTo(260,502);}
      else
        {contexto.lineTo(i+260,500-y2);}
      x1=x2;
      x2=x2+0.2;
     }
 
    x1=0;
    x2=-0.2;
    y1=0;
    y2=0;
    for(var i=0;i<=rmax;i++){
      y1=(Math.pow(x1,4)*0.000000001*constante)*5
      y2=(Math.pow(x2,4)*0.000000001*constante)*5
      if (i==0){
        contexto.moveTo(260,500);}
      if (i==rmax){
        contexto.lineTo(-i+260,502);
        contexto.lineTo(260,502);
       }
      else{
        contexto.lineTo(-i+260,500-y2);
       }
      x1=x2;
      x2=x2-0.2;
    }
    contexto.stroke();
    contexto.fill();
    contexto.closePath();
    if (contador==0) {
      fechaHora1 = new Date();
      horas1 = fechaHora1.getHours();
      minutos1 = fechaHora1.getMinutes();
      segundos1 = fechaHora1.getSeconds();
      tiempo_1=horas1*60*60+minutos1*60
      +segundos1;
     }
    if (contador<=500 && contador>0) {
      fechaHora2 = new Date();
      horas2 = fechaHora2.getHours();
      minutos2 = fechaHora2.getMinutes();
      segundos2 = fechaHora2.getSeconds();
      tiempo_2=horas2*60*60+minutos2*60+
      segundos2;
      tiempo_3=tiempo_2-tiempo_1;
      if (tiempo_3==1){
        document.getElementById('reloj2').
        innerHTML = tiempo_3+' segundo';}
      else
        {if (contador==500)
          {document.getElementById
        ('reloj2').innerHTML = tiempo+' segundos';}
        else
          {document.getElementById('reloj2')
          .innerHTML = tiempo_3+' segundos';}
         }
     }
     if (contador<= 500){
       contexto2.strokeStyle='blue';
       contexto2.fillStyle='#8f00e3';
       contexto2.fillRect(0,0,600,600);
       contexto2.fillStyle='blue';
       contexto2.beginPath();
       contexto2.moveTo(rmax+260,contador);
       contexto2.lineTo(rmax+260,500);
       contexto2.lineTo(260-rmax,500);
       contexto2.lineTo(260-rmax,contador);
       contexto2.lineTo(rmax+260,contador);
       contexto2.stroke();
       contexto2.fill();
       contexto2.closePath();}
       contador=contador+1;}
    }
}